Operations Research - IMK Engineering – Ingenieurbüro für Mechatronik und Kybernetik Dr. Bruns
Hauptmenü:
Kompetenzen
Kompetenzen ⇒ Operations Research
„Operations Research ist geprägt durch die Zusammenarbeit von Mathematik, Wirtschaftswissenschaften und Informatik.“ (Gesellschaft für Operations Research e.V.) | ||
Die Fachgebiete Optimierung und Operations Research sind einander sehr ähnlich, da in beiden Gebieten nahezu dieselben mathematischen Verfahren zum Einsatz kommen. Wenn es darum geht, technische Systeme oder Prozesse zu optimieren oder deren Parameter zu identifizieren, dann wird zumeist von Optimierung gesprochen. Stehen wirtschaftliche Überlegungen oder die Optimierung betriebswirtschaftlicher Prozesse im Vordergrund, so ist häufig von Operations Research die Rede. Methoden des Operations Research kommen auch bei komplexen Problemstellungen im Rahmen von Entscheidungsprozessen (Decision Support) zum Einsatz. Dann geht es darum, mit Hilfe adäquater mathematischer Methoden die möglichst optimale Entscheidung zu treffen.
Im Folgenden werden einige Verfahren und Beispiele kurz vorgestellt, die primär bei betriebswirtschaftlichen Prozessen und Überlegungen Anwendung finden, also letztlich bei dem Wunsch nach Kostenminimierung, generell aber auch für die Optimierung technischer Systeme und Prozesse eingesetzt werden können und teilweise auch schon eingesetzt werden:
„Für die Umsetzung der Digitalen Agenda der Bundesregierung (Industrie 4.0 etc.) sind die Methoden aus den Bereichen der Optimierung und des Operations Research ein wichtiger Baustein.“ (IMK Engineering) |
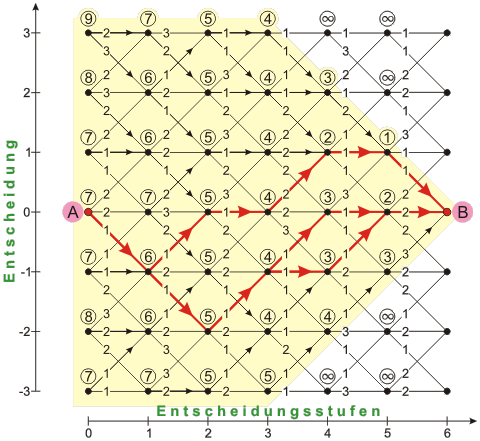
Bild 1: Dynamische Programmieruing (Rückwärtsrekursion von B nach A)
Lineare Optimierung
Die lineare Optimierung wird auch als Lineare Programmierung (LP) oder als Lineare Planungsrechnung bezeichnet. Die mathematischen Modelle bestehen i.d.R. aus linearen Zielfunktionen mit ebenfalls linearen Nebenbedingungen. Die lineare Optimierung wird in unterschiedlichsten Unternehmensbereichen angewendet, beispielsweise im Bereich der Fertigungsplanung, wo sie im Rahmen von Produktionsprogramm-, Mischungs- und Verschnittoptimierung eingesetzt wird. Das wichtigste mathematische Verfahren für die Lösung linearer Optimierungsaufgaben ist der Simplex-Algorithmus. Für Probleme der Linearen Optimierung mit spezieller Struktur, die häufig im Bereich der Logistik (Transport-, Umlade- oder Netzwerkflussprobleme) auftreten, existieren eine große Zahl weiterer Verfahren, die teilweise auch in das Gebiet der Graphentheorie fallen.
| Optimierungsaufgabe | |
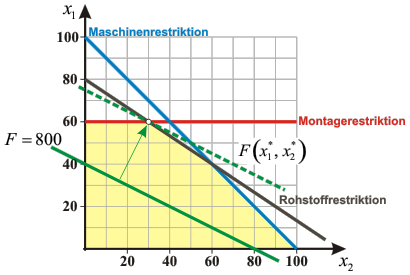
| Maximiere | $F\left( {{x_1},\;{x_2}} \right) = 10{x_1} + 20{x_2}$ |
| Nebenbedingungen | |
Maschinenrestriktion: | ${x_1} + {x_2} \le 100$ |
Rohstoffrestriktion: | $6{x_1} + 9{x_2} \le 720$ |
Montagerestriktion: | ${x_2} \le 60$ |
${x_1},\;{x_2} \ge 0$ |
Ein simples Beispiel: Produktionsprogrammpalnung
Ein Unternehmen kann in einer Periode $x_1$ Mengeneinheiten (ME) des Produkts $P_1$ herstellen sowie $x_2$ ME des Produkts $P_2$. Das Produkt $P_1$ weist einen Deckungsbeitrag von $10$ Geldeinheiten (GE) je Stück auf, bei dem Produkt $P_2$ sind es $20$ GE. Die Maschinenkapazität ist auf $100$ Leistungseinheiten je Periode beschränkt. In beiden Produkten wird derselbe Rohstoff verarbeitet, von dem in dieser Periode exakt $720$ Einheiten verfügbar sind. Ferner können in der Montageabteilung maximal $60$ ME des Produkts $P_2$ produziert werden.
Graphische Lösung
LP mit spezieller Struktur
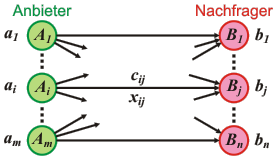
Es gibt Probleme der Linearen Optimierung, die aufgrund ihrer Nebenbedingungen eine spezielle Struktur aufweisen und für die deshalb auch spezielle Lösungsverfahren entwickelt wurden bzw. verfügbar sind, welche die Probleme rechnerisch effizienter lösen, als es mit dem Simplex-Algorithmus möglich ist. Zu diesen Optimierungsproblemen gehören bspw. das klassische Transportproblem (siehe nebenstehende Graphik), das lineare Zuordnungsproblem (bspw. Zuordnung von Arbeiten zu Arbeitern oder Maschinen bei festen Ausführungskosten ) sowie das Umladeproblem.
Das klassische Transportproblem
Graphentheorie
Die Graphentheorie ist ein äußerst vielseitiges Instrumentarium und kann auf unterschiedlichste Fragestellungen angewendet werden. Beispielsweise lassen sich mit Methoden der Graphentheorie Organisationsstrukturen und Projektabläufe graphisch anschaulich darstellen und analysieren. Die Graphentheorie wird aber auch genutzt, um sogenannte „kürzeste Wege“ sowie „maximale oder kostenminimale Flüsse“ in Graphen bzw. Netzwerken aufzufinden (Netzwerkflussprobleme). Algorithmen für die Berechnung kürzester Wege kommen in jedem Navigationssystem zum Einsatz, wenn ein distanz-, kosten- oder zeitoptimaler Weg von einem bestimmten Ort zu einem beliebigen anderen Ort berechnet werden soll. Immer dann, wenn eine oder mehrere Entitäten in einem Netzwerk mit oder ohne Kapazitätsgrenzen optimal, egal ob distanz-, kosten- oder zeitoptimal, bewegt werden sollen, dann sollten die Methoden der Graphentheorie zuerst auf ihre Anwendbarkeit hin geprüft werden.
Dies ist beispielsweise auch der Fall, wenn ein Evakuierungsplan für ein Bürogebäude erstellt werden soll. Die einzelnen Büros sind über Flure und Treppen zu einem Netzwerk verbunden, wobei Kapazitätsgrenzen zu berücksichtigen sind. Im Notfall müssen sämtliche Leute in den Büros durch dieses Netzwerk möglichst schnell zum Gebäudeausgang gelangen.
Im Rahmen des Kreuzungsmanagements werden optimale Geschwindigkeitsprofile für Fahrzeuge mit Ansätzen aus dem Bereich der Graphentheorie und der Dynamischen Programmierung (DP) berechnet. Diese Geschwindigkeitsprofile garantieren Kollisionsfreiheit und optimieren parallel andere Zielgrößen wie Kraftstoffverbrauch, Komfort und Dauer. Die Laufzeit des Algorithmus ist ferner deterministisch und skalierbar.
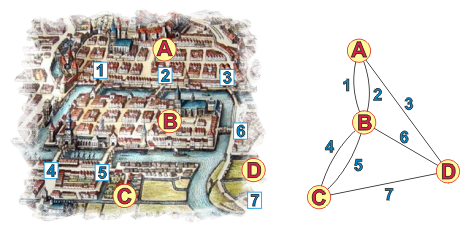
Anfänge der Graphentheorie: Das Königsberger Brückenproblem
Das Königsberger Brückenproblem ist eine mathematische Fragestellung, die anhand von sieben Brücken der Stadt Königsberg illustriert wurde. Zu klären war, ob es einen Weg gibt, bei dem man alle sieben Brücken über den Fluss Pregel genau einmal überquert, und wenn ja, ob auch ein Rundweg möglich ist, bei dem man wieder zum Ausgangspunkt gelangt. Leonhard EULER bewies 1736, dass ein solcher Weg nicht existiert.
EULER wird häufig als Begründer der Graphentheorie genannt. Er wurde jedoch seinerseits durch Ausführungen von Gottfried Wilhelm LEIBNIZ aus dem Jahre 1679 inspiriert. LEIBNIZ nannte die Disziplin, die von EULER "wiederentdeckt" wurde und später in der Graphentheorie aufging, die Geometrie der Lage.
Graph bzw. Netzwerk
(hier für die Suche nach einem "kürzesten Weg")
Das "Königsberger Brückenproblem"
Ganzzahlige (lineare) und kombinatorische Optimierung
Bei der linearen Programmierung (LP), die zuvor beschrieben wurde, werden die Variablen des Optimierungsproblems ausschließlich als kontinuierliche Variablen betrachtet. Im Gegensatz dazu können bei Optimierungsproblemen der ganzzahligen und kombinatorischen Optimierung die Variablen nur diskrete ganzzahlige Werte annehmen.
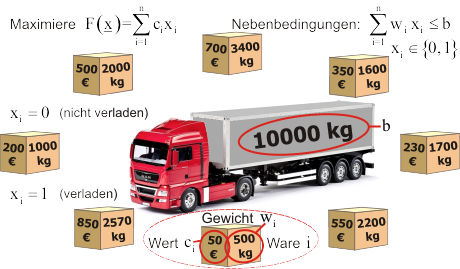
Wird die Menge dieser diskreten Werte auf die Werte $0$ und $1$ beschränkt, so lassen sich auch binäre Optionen formulieren. Beispiele dafür sind das Rucksack- oder Knapsack-Problem sowie Standortprobleme in Netzen. Auch Probleme der Investitionsplanung werden häufig mit binären Variablen formuliert: Investition in Maschine $i$? (ja: $x_i=1$; nein: $x_i=0$).
Im Folgenden sind einige Beispiele aufgeführt, bei denen Algorithmen aus dem Bereich der ganzzahligen und kombinatorischen Optimierung bevorzugt zur Anwendung kommen.
"Rucksack"-Problem
Zuordnungsprobleme
- Innerbetrieblichen Standortplanung: Die Zuordnung von Maschinen zu Plätzen ist so zu bestimmen, dass bei innerbetrieblichen Transporten zwischen den Maschinen die Transportkosten minimiert werden.
- Stundenplanproblem: Es ist eine zulässige Zuordnung von Lehrern zu Klassen und Räumen zu bestimmten Zeiten festzulegen.
Reihenfolgeprobleme
- „Traveling Salesman“-Problem: Die Aufgabe besteht darin, eine Reihenfolge für die Anfahrt mehrerer Orte zu finden, bspw. im Rahmen einer Warenauslieferungstour, bei der die erste Station identisch ist mit der letzten Station (Rundreise) und die zurückgelegte Gesamtstrecke und/oder die Gesamtkosten minimal sind.
- Briefträger-Probleme („Chinese Postman“-Problem): Sämtliche Straßen eines Zustellbezirks sollen optimal durchlaufen werden.
- Allgemeine Tourenplanungsprobleme: Die Belieferung von Kunden durch mehrere Fahrzeuge eines Möbelhauses soll optimal gelöst werden, indem die gesamte zurückgelegte Entfernung sämtlicher Fahrzeuge minimiert wird.
- Maschinenbelegungsprobleme: Bestimmung einer Auftragsreihenfolge, so dass die Summe zeitlicher Überschreitungen von zugesagten Fertigstellungsterminen minimal wird.
Gruppierungsprobleme
- Fließbandabstimmung: Zusammenfassung und Zuordnung von Arbeitsgängen zu Bandstationen.
- Losgrößenplanung: Zusammenfassung periodenbezogener Nachfragen zu Beschaffungs- bzw. Fertigungslosen.
- Clusteranalyse: Bildung von möglichst ähnlichen Kundengruppen hinsichtlich eines bestimmten Bewertungsmaßes.
- Zuschnitt und Verpackungsprobleme („Cutting and Packing“)
Auswahlprobleme
- Rucksack- bzw. Knapsack-Problem: Bei begrenzter Transportkapazität können unterschiedliche Güter mit unterschiedlichem Wert transportiert werden. Unter Berücksichtigung der Kapazitätsbeschränkung soll die Güterzusammenstellung mit dem größten Wert bzw. Nutzen ermittelt werden. (Dieses Problem lässt sich auch mit Methoden der Dynamischen Programmierung formulieren und lösen.)
- „Set Partitioning“- und „Set Covering“-Probleme: Auswahl einer kostenminimalen Menge von Auslieferungstouren aus einer großen Anzahl möglicher Touren. Weiterhin lassen sich viele Zuordnungs- und Reihenfolgeprobleme häufig auch als Auswahlproblem formulieren und mit entsprechenden Methoden und Algorithmen lösen.
Dynamische Optimierung (Dynamische Programmierung)
Die Dynamische Optimierung wird allgemein auch als Dynamische Programmierung (DP) bezeichnet und geht auf den amerikanischen Mathematiker Richard BELLMAN zurück. Sie ist ein Optimierungsverfahren aus dem Bereich der diskreten Mathematik, mit starker Anlehnung an das Teilgebiet der Graphentheorie. BELLMAN selbst spricht davon, dass man sie, von einem gewissen Standpunkt aus gesehen, mehr als eine bestimmte Art zu denken denn als ein festes System von mathematischen Regeln und Vorschriften auffassen kann. Der Grund für diese Aussage liegt wohl darin, dass vielfach die mit der Dynamischen Programmierung verbundene Herausforderung bei der Lösung eines Optimierungsproblems nicht in der mit der Lösungsberechnung verbundenen Mathematik bzw. Algorithmik gesehen wird, sondern vielmehr in der adäquaten Modellierung der Problemstellung, so dass die Methode der Dynamischen Programmierung überhaupt erst auf das gegebene Problem anwendbar wird.
Voraussetzung für die Anwendung ist ein mehrstufiger Entscheidungsprozess im Sinne von mehreren Entscheidungen, die nacheinander zu treffen sind. Das Problem des Auffindens der optimalen Gesamtstrategie $J^*$ kann dann auf Basis des „BELLMAN’schen Optimalitätsprinzips“ auf das Auffinden von optimalen Teilstrategien reduziert werden. Dadurch wird die Komplexität des Optimierungsproblems stark reduziert. Dieses Prinzip wird gelegentlich auch als „Teile und herrsche“ bezeichnet, das für eine Vielzahl von Algorithmen in der Informatik die Basis bildet. Das Gesamtproblem wird dann in einem iterativ rekursiven Prozess sukzessive über die einzelnen Entscheidungstufen hinweg gelöst. Zur Anwendung kommen die sogenannte „Rückwärtsrekursion“ oder die „Vorwärtsrekursion“, je nach Problemstellung.
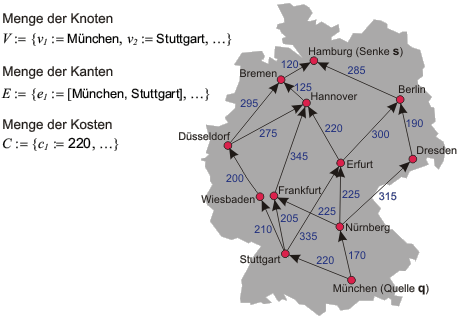
Das Problem von oben (Graphentheorie; Kürzester Weg von München nach Hamburg), formuliert gemäß der Dynamischen Programmierung (DP):

Das BELLMAN'sche Optimalitätsprinzip „Die Gesamtstrategie kann nur dann optimal sein, wenn jede Teil- bzw. Reststrategie optimal ist, ganz gleich, von welchem Zwischenzustand sie ausgeht.“ (Richard BELLMAN) | |||||
Die Anwendungsbereiche der Dynamischen Programmierung sind äußerst vielschichtig. Beispielsweise wird sie im betriebswirtschaftlichen Rahmen für die Planung von Bestellmengen und Losgrößen eingesetzt. Im Bereich der Regelungstechnik wird sie genutzt, um eine optimale Trajektorie (s. a. Optimale Steuerung) für die Überführung eines dynamischen Systems in einen gewünschten Systemzustand zu berechnen. Im Bereich des Kreuzungsmanagements wurde sie für die Formulierung des Optimierungsproblems verwendet, das später mit einem „Kürzeste Wege“-Algorithmus aus der Graphentheorie gelöst wurde.
Erklärung des Optimalitätsprinzips an einem Beispiel aus der Routenplanung
Hat man einen optimalen bzw. kürzesten Weg $J^*$ von der Stadt $A$ zur Stadt $B$ gefunden, der über die Städte $X$ und $Y$ führt, so muss auch der Weg zwischen den Städten $X$ und $Y$ optimal sein bzw. der kürzesten Verbindung dieser beiden Städte entsprechen. Wäre dies nicht der Fall, so könnte $J^*$ verkürzt werden, indem man zwischen den Städten $X$ und $Y$ einen kürzeren Teilweg verwenden würde. $J^*$ wäre in diesem Fall dann aber nicht optimal.
Warteschlangentheorie
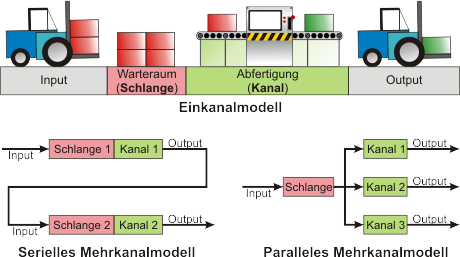
Bei der Warteschlangentheorie geht es um das Abfertigungsverhalten von Service- und Bedienstationen. Dabei kann es sich sowohl um Kundenschlagen in Supermärkten, an Bank- und Behördenschaltern als auch um Pufferlager von Bauteilen vor Maschinen handeln.
Zumeist sind es die betriebliche Kosten bzw. der Wunsch, diese zu minimieren, der zu einer Untersuchung von Systemen mit Warteschlange führt. Das Ziel ist dann, die Ursache für das Auftreten von Warteschlangen zu identifizieren und Möglichkeiten einer verbesserten Um- oder Neugestaltung aufzuzeigen.
Das Warteschlangensystem wird als Input-Output-System mit Warteraum und Abfertigung (Bild) beschrieben. Für die Beschreibung von Ankunfts- und Abfertigungsprozessen wird häufig die Binomialverteilung verwendet, die aufgrund des hohen Rechenaufwands wiederum in der Vergangenheit häufig mit der Poisson-Verteilung approximiert wurde. Die Exponentialverteilung wird vielfach für die Beschreibung des zeitlichen Abstands zweier unmittelbar aufeinander folgender Input-Entitäten (Kunden, Bauteile bzw. Werkstücke etc.) verwendet.
Wichtige Kenngrößen eines Wartesystems sind beispielsweise:
- ⌀ Systemlänge (Elemente in Warteraum und Abfertigung)
- ⌀ Schlangenlänge (Elemente im Warteraum)
- ⌀ Verweilzeit im System
- ⌀ Wartelänge im Warteraum
Warteschlangenmodelle
Gleichgewichtsmatrix einer homogenen Markovkette
\[ \mathop {\lim }\limits_{n \to \infty } \;\;{P^n} = \bar P = \left( {{{\bar p}_{ij}}} \right) \]
Binomialverteilung \[ f_B\left( x \right) = B\left( {n,p} \right) = \left( \begin{matrix} n\\ x\\ \end{matrix} \right) \cdot {p^x} \cdot \left( {1-p} \right)^{n-x} \] |
Poisson-Verteilung \[ f_P\left( x \right) = \frac{{{\gamma ^x}}}{{x!}}{e^{ - \gamma }} \] | Exponentialverteilung \[ f_E\left( x \right) = \delta {e^{ - \delta x}} \] |
(Stochastische) Simulation
Die Simulation ist ein experimenteller Zweig des Operations Research und dient dort primär der Analyse stochastischer Problemstellungen. Dies ist zwar zu unterscheiden von der Anwendung der Simulation im Bereich „Modellbildung & Simulation“, wo es primär um die Beschreibung des Verhaltens dynamischer Systeme geht, häufig durch ein System von Differentialgleichungen, generell gehen aber diese beiden Gebiete der Simulation fließend ineinander über. Folgende Klassifikation kann vorgenommen werden:
- Diskrete Simulation: Die diskrete Ereignis-Simulation befasst sich mit der Modellierung und der Simulation dynamischer Systeme.
- Kontinuierliche Simulation: Hier steht das kontinuierliche Verhalten dynamischer Systeme im Vordergrund, was in der Regel mit einem System von Differentialgleichungen beschrieben wird.
- Stochastische Simulation: Hier stehen Wahrscheinlichkeiten für das Auftreten bestimmter Ereignisse und deren Konsequenzen im Fokus der Analyse. Die „Monte Carlo“-Simulation ist hier ein bekannter und wichtiger Vertreter.
Die stochastische Simulation dient der Vorhersage der Zustände eines Systems, die in diesem Fall von einer Menge von Einflussfaktoren abhängen, die durch Wahrscheinlichkeitsverteilungen beschrieben werden, bspw. die Wahrscheinlichkeit für den Ausfall einer Maschine oder die Ankunft neuer Bauteile im Vorpuffer einer Maschine. Typische Anwendungsfälle sind die Folgenden:
- Analyse eines Warteschlangensystems oder einer Vernetzung mehrerer dieser Systeme.
- Analyse von Lagerhaltungsproblemen bei stochastischer Nachfrage und/oder Lieferzeiten.
- Auswertung stochastischer Netzpläne mit stochastischen Vorgangsdauern und/oder Vorgangsfolgen.
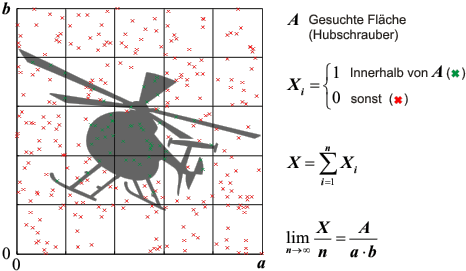
Integration einer Fläche mittels stochastischer Simulation
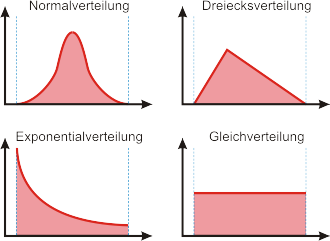
Einige wichtige Funktionen f(x) der Wahrscheinlichkeitsdichte
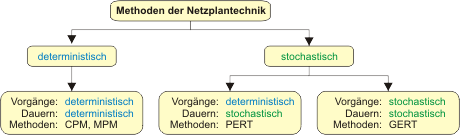
Netzplantechnik
Die Netzplantechnik ist primär eine Methode der Planung und kommt dabei im Rahmen von Strukturplanungen, Zeit- oder Terminplanungen sowie Kosten- und/oder Kapazitätsplanungen zum Einsatz. Ferner wird sie bei der Überwachung und der Kontrolle von betrieblichen Abläufen und komplexen Projekten eingesetzt.
Anwendungsbeispiele:
- Projekte im Bereich der Forschung und der Entwicklung,
bspw. Entwicklung eines neuen Fahrzeugs oder Flugzeugs - Bauprojekte (Kraftwerke, Fabriken, Flughäfen ...)
- Projekte der betrieblichen Organisation,
bspw. Einführung eines neuen Softwarepakets - Kampagnen (Werbe- oder Wahlkampagnen, ...)
- Planung von Großveranstaltungen (Weltmeisterschaft, ...)
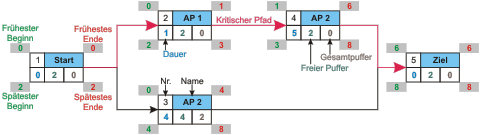
- CPM (Critical Path Method)
- MPM (Metra Potential Method)
- PERT (Program Evaluation and Review Technique)
Methoden der Netzplantechnik
Beispiel für einen Netzplan (CPM)